Page 23 - bilim_dergisi

Aycan vd. Denizli İl Millî Eğitim Müdürlüğü Bilim ve Eğitim Dergisi 1(1), 2025 *Hatice Nur KOÇ

1. Giriş

1.1. Taxicab Geometri’nin Tarihçesi

Taxicab geometri, bazı kaynaklarda L1 metriği olarak da adlandırılır. L1 metriği, 1757'de Roger Joseph Boscovich
tarafından regresyon analizinde kullanılmıştır. Taxicab geometrinin geometrik yorumu, Hermann Minkowski'nin
Minkowski eşitsizliği ile Öklid dışı geometrilerin gelişmesine kadar uzanır (Krause, 1986).
İlk olarak Taxicab geometrisini incelemek için gerçek dünyadan kaynaklanan sorular ortaya çıktı . Apartmanlar,
fabrikalar, telefon kulübeleri gibi yerlerin optimum konumlarıyla ilgili sorular bir dizi geometrik soruna neden oldu.
Taxicab geometri alanın tamamen Öklid uzaklık fonksiyonu dE yerine Taxicab uzaklık fonksiyonu dT ile değiştirilmesiyle
ortaya çıkar. Bu tür bir değişiklik, uzaklık fonksiyonunun nasıl hesaplanacağı, açı özelliklerinin ne olacağı gibi yeni
soruların keşfedilmesine yol açar.

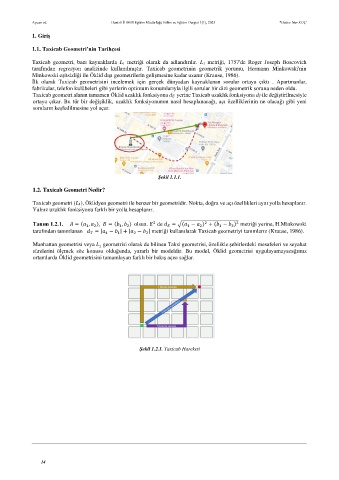
Şekil 1.1.1.

1.2. Taxicab Geometri Nedir?

Taxicab geometri (L1), Öklidyen geometri ile benzer bir geometridir. Nokta, doğru ve açı özellikleri aynı yolla hesaplanır.
Yalnız uzaklık fonksiyonu farklı bir yolla hesaplanır.

2
Tanım 1.2.1. = ( , ), = ( , ) olsun. de = √( − ) + ( − ) metriği yerine, H.Minkowski
2
2
1
2
1

2
1
2
1
2
tarafından tanımlanan = | − | + | − | metriği kullanılarak Taxicab geometriyi tanımlarız (Krause, 1986).
2
1
1

2
Manhattan geometrisi veya geometrisi olarak da bilinen Taksi geometrisi, özellikle şehirlerdeki mesafeleri ve seyahat
1
sürelerini ölçmek söz konusu olduğunda, yararlı bir modeldir. Bu model, Öklid geometrisi uygulayamayacağımız
ortamlarda Öklid geometrisini tamamlayan farklı bir bakış açısı sağlar.

Şekil 1.2.1. Taxicab Hareketi

14