Page 26 - bilim_dergisi

Aycan vd. Denizli İl Millî Eğitim Müdürlüğü Bilim ve Eğitim Dergisi 1(1), 2025 *Hatice Nur KOÇ

Şekil 2.3.1 Taxicab Parabol

2.4. Taxicab Hiperbol

Tanım 2.4.1. Analitik düzlemde odak noktası olarak adlandırılan sabit iki noktaya uzaklıkları farkı mutlak değerce,
sabit olan noktaların geometrik yerine hiperbol adı verilir (Kaya, 2002).
= { ( , )| ( , ) − ( , ) = 2 }
1
2
Burada Öklidyen anlamda uzaklık fonksiyonudur.

Tanım 2.4.2. Taxicab geometrisinde, iki nokta arasındaki mesafe şu şekilde tanımlanır:

(( , ), ( , )) = | − | + | − |
1
2
2
1
1
2
1
2
Taxicab hiperbol, bu mesafe fonksiyonuna göre sabit bir fark veren iki nokta kümesini tanımlar.

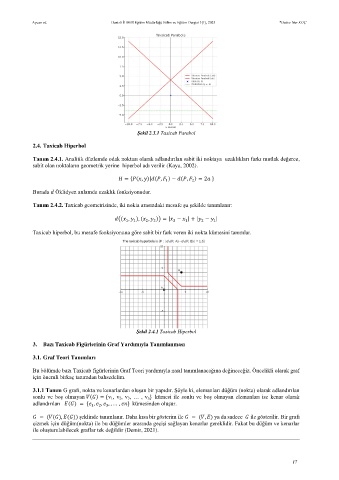
Şekil 2.4.1 Taxicab Hiperbol

3. Bazı Taxicab Figürlerinin Graf Yardımıyla Tanımlanması

3.1. Graf Teori Tanımları
Bu bölümde bazı Taxicab figürlerinin Graf Teori yardımıyla nasıl tanımlanacağına değineceğiz. Öncelikli olarak graf
için önemli birkaç tanımdan bahsedelim.

3.1.1 Tanım G grafı, nokta ve kenarlardan oluşan bir yapıdır. Şöyle ki, elemanları düğüm (nokta) olarak adlandırılan
sonlu ve boş olmayan ( ) = {v1, v2, v3, … , vn} kümesi ile sonlu ve boş olmayan elemanları ise kenar olarak
adlandırılan ( ) = { , , , , … , } kümesinden oluşur.
1
2
3
= ( ( ), ( )) şeklinde tanımlanır. Daha kısa bir gösterim ile = ( , ) ya da sadece ile gösterilir. Bir grafı
çizmek için düğüm(nokta) ile bu düğümler arasında geçişi sağlayan kenarlar gereklidir. Fakat bu düğüm ve kenarlar
ile oluşturulabilecek graflar tek değildir (Demir, 2021).

17