Page 24 - bilim_dergisi

Aycan vd. Denizli İl Millî Eğitim Müdürlüğü Bilim ve Eğitim Dergisi 1(1), 2025 *Hatice Nur KOÇ

Örnek 1

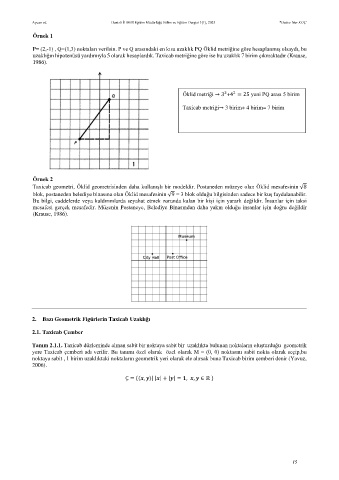
P= (2,-1) , Q=(1,3) noktaları verilsin. P ve Q arasındaki en kısa uzaklık PQ Öklid metriğine göre hesaplanmış olsaydı, bu
uzaklığın hipotenüsü yardımıyla 5 olarak hesaplardık. Taxicab metriğine göre ise bu uzaklık 7 birim çıkmaktadır (Krause,
1986).

2
2
Öklid metriği → 3 +4 = 25 yani PQ arası 5 birim
Taxicab metriği→ 3 birim+ 4 birim= 7 birim

Örnek 2
Taxicab geometri, Öklid geometrisinden daha kullanışlı bir modeldir. Postaneden müzeye olan Öklid mesafesinin √8
blok, postaneden belediye binasına olan Öklid mesafesinin √9 = 3 blok olduğu bilgisinden sadece bir kuş faydalanabilir.
Bu bilgi, caddelerde veya kaldırımlarda seyahat etmek zorunda kalan bir kişi için yararlı değildir. İnsanlar için taksi
mesafesi gerçek mesafedir. Müzenin Postaneye, Belediye Binasından daha yakın olduğu insanlar için doğru değildir
(Krause, 1986).

2. Bazı Geometrik Figürlerin Taxicab Uzaklığı

2.1. Taxicab Çember

Tanım 2.1.1. Taxicab düzleminde alınan sabit bir noktaya sabit bir uzaklıkta bulunan noktaların oluşturduğu geometrik
yere Taxicab çemberi adı verilir. Bu tanımı özel olarak özel olarak M = (0, 0) noktasını sabit nokta olarak seçip,bu
noktaya sabit , 1 birim uzaklıktaki noktaların geometrik yeri olarak ele alırsak buna Taxicab birim çemberi denir (Yavuz,
2006).

Ç = {( , )| | | + | | = , , ∈ ℝ }

15